
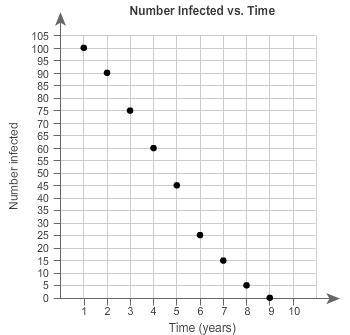
Wilcox, in Introduction to Robust Estimation and Hypothesis Testing (Fifth Edition), 2022 9.4.5 R Functions scor, scorall, scorci, mscorpb, mscorci, mscorciH, scorreg, scorregci, and scorregciH It is straightforward to imagine that a similar effect occurs when one projects multivariate data on two dimensions. Three outliers are added it can be seen that a projection of the data onto either one of both axes does only reveal one of the three outliers. In Figure 1, a bivariate distribution is plotted. Consider the reduction of a bivariate problem to one variable. Even then the outliers can be of a multivariate nature such that they will not be detected by inspecting only two dimensions. Visual inspection by simply plotting the data is practically impossible as one would need to inspect plots of all possible pairs of two variables. In particular, chemometric calibration and classification problems are usually of a high-dimensional nature: For example, in spectrophotometry, the spectra are commonly measured at p > 1000 variables.
For multivariate data clouds, it will be difficult or even impossible to visualize the data and graphically detect the outliers. The functionĭetection of either multimodality or outliers is straightforward for univariate and bivariate data. It is a polygon (a convex hull) containing the central half of the data as measured by the depth of the points. If simultaneously pts is not specified, m contains two columns of data (so bivariate data are being analyzed), and plotit=T, a scatterplot of the data is created that marks the center of the data corresponding to the location estimator specified by the argument cop, and it creates what Liu, Parelius, and Singh (1999, p. Setting cop=3 results in using the marginal medians, cop=4 uses the MVE estimator (discussed in Section 6.3.1). The argument cop indicates the location estimator, θ ˆ, that will be used by method A1. (For p = 1, the exact halfspace depth is computed by calling the function unidepth.) If pts is not specified, the function returns the halfspace depth of all points in m. In some key instances, we will specifically indicate how the bivariate equations can be adapted for the general multivariate case.Ĭomputes the approximate halfspace depth of all the points in pts relative to the data in m using method A1. Equations for generalized multivariate data are cumbersome and difficult to read and grasp. In this chapter, we will concentrate on bivariate data as such data are still the most commonly used. There is no reason to further distinguish between tervariate and higher variate data the reason being that matrix notation is directly applicable to bivariate data only and there is no equivalent notation for higher variate data structures.
#NO ASSOCIATION SCATTER PLOT SOFTWARE#
Often, it is possible to rearrange multivariate data as bivariate data although this is not crucial, it allows the structure of matrix-based software to be maintained.
Multivariate data consist of individual measurements that are acquired as a function of more than two variables, for example, kinetics measured at many wavelengths and as a function of temperature, or as a function of pH, or as a function of initial concentrations, and so forth, of the reacting solutions. Advantages include compact notation and the efficient implementation of the numerical analysis algorithms into matrix-based software such as Matlab. The structures of bivariate data for most of the above kind lend themselves to very elegant matrix notation. Other alternatives include nuclear magnetic resonance (NMR) and electron paramagnetic resonance (EPR) spectroscopies or electrochemical data such as polarograms or voltamograms. Absorption measurements in the near-infrared (NIR) and mid-IR are of the same nature but less commonly acquired. By far the most common measuring technique that delivers bivariate data is absorption spectroscopy in the ultraviolet–visible (UV-Vis) region of the electromagnetic spectrum. (a) A monovariate data set (b) a bivariate data set (c) a multivariate data set.īivariate data are measurements taken as a function of two independent variables a typical example would be absorption spectra taken by a diode array detector in liquid chromatography where the independent variables are chromatographic time and wavelength. Discount and origination points have been combined.įigure 1. Source: Data are for a loan to borrow $300,000 in Seattle for 30 years at a fixed rate, accessed at on July 15, 2010. Census Bureau, Statistical Abstract of the United States: 2010 (129th edition), Washington, DC, 2009, accessed at on July 16, 2010.


 0 kommentar(er)
0 kommentar(er)
